УДК 373.3.016:51

Пачинчик Ю.Ю.

студентка 4 курса педагогического факультета

Учреждения образования «Гродненский государственный университет имени Янки Купалы»

(Научный руководитель – Гадзаова С.В., старший преподаватель кафедры естественнонаучных и лингвистических дисциплин и методик их преподавания УО «ГрГУ им. Я. Купалы»)

КОМПЛЕКС УЧЕБНЫХ ЗАДАНИЙ КАК СРЕДСТВО РЕАЛИЗАЦИИ ДИФФЕРЕНЦИРОВАННОГО ПОДХОДА НА УРОКАХ МАТЕМАТИКИ

В 3 КЛАССЕ

 

Аннотация. В данной статье рассматривается реализация дифференцированного подхода посредством комплекса учебных заданий на уроках математики в 3 классе.

 

В связи со становлением новых экономических и общественных отношений в Беларуси наблюдается изменение отношения к общечеловеческим ценностям, в том числе и к знаниям. Если взрослые люди осознают важность получения образования и видят в нем залог будущей экономической самостоятельности, то среди молодежи, наоборот, резко снизился интерес к учению.

Перед школой стоит сложная задача повышения интереса к учению, в частности, к математике, как основе развития личности. Особую актуальность на данном этапе развития системы образования приобретают разработка и внедрение в школьную жизнь различных форм дифференциации, индивидуализированной педагогической помощи младшим школьникам.

Для восполнения пробелов в знаниях учащихся и устранения фактических ошибок эффективно использовать дифференцированные задания с нарастающей степенью сложности. В каждом варианте таких заданий выделяются наиболее трудные вопросы, которые могут служить причиной ошибок. В системе упражнений, переходя от работы под непосредственным руководством учителя к частичной и далее к полностью самостоятельной работе, учащиеся постепенно справляются с заданиями разной степени трудности. При этом трудность задания и степень самостоятельности его выполнения постепенно нарастают. Результаты этой кропотливой работы скажутся довольно быстро.

Применение дифференцированных заданий при обучении математике весьма актуально. Не все обучающиеся имеют одинаковый интерес к изучаемому предмету, у них разные способности, не каждый может проявить собственное «Я». Предлагаемый подход помогает обучающимся создать для себя на уроке «ситуацию успеха» благодаря личностному выбору [1, с. 211].

Предлагаемый подход помогает обучающимся создать для себя на уроке «ситуацию успеха» благодаря личностному выбору. Кроме того, он позволяет выявить не только конкретные знания по теме, но и проверить усвоение их в комплексе, прогнозировать результаты обучения, создает возможность для творческого применения знаний, являясь побудительным мотивом к дальнейшему росту и самосовершенствованию [2].

Учитель при проектировании данной образовательной среды сам определяет цель развития обучающегося, стараясь учесть индивидуальность каждого, не предъявляет цель в явном виде, а концентрирует внимание на способах организации самостоятельной активности для ее достижения.

При разработке разноуровневых заданий были учтены четыре уровня подготовки учащихся: ученический, алгоритмический, эвристический и творческий. На протяжении всего педагогического эксперимента учащимся предлагались задания, соответствующие их уровню.

Задания ученического уровня направлены на формирование репродуктивных умений в стандартной ситуации. Они обеспечивает правильность знаний, то есть правильное выполнение аналогичных заданий без собственных комментариев. Задания алгоритмического уровня формируют репродуктивные умения в измененной ситуации. Они обеспечивают полноту и действенность знаний, то есть учащийся может перечислить все ведущие элементы знаний, дать определение каждому из них, охарактеризовать основные их признаки, а также выполнить задания по теме с применением полученных знаний и умений. Задания эвристического уровня способствуют формированию исследовательских умений в нестандартной ситуации. Задания творческого уровня рассчитаны на формирование творческих умений. Задания эвристического и творческого уровня обеспечивают также осознанность, системность и прочность знаний. Сюда относятся задания познавательно-поискового характера, в процессе выполнения которых учащиеся приобретают новые знания.

Нами был разработан комплекс заданий, разделенный на несколько групп в соответствии с основными содержательными линиями начального курса математики:

А) Задания для этапа устного счета:

Задания для ученического уровня:

Реши уравнения: x + 20 = 60, 100 – y = 25

Задания для алгоритмического уровня:

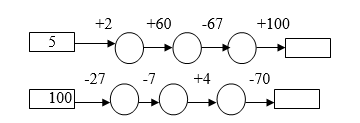
Реши цепочки примеров:

      

Задания для эвристического уровня:

Реши задачу: «Кате 5 лет, а ее старшему брату – на 5 больше. Через 17 лет Кате будет 22 года. Сколько лет будет ее брату?»

Реши задачу: «Каменщик за час укладывает 100 кирпичей, а его ученик на 40 кирпичей меньше. Сколько кирпичей они укладывают вместе?»

Задания для творческого уровня:

Реши задачу: «Жили три девочки в одном доме. Их звали Маша, Юля и Карина, и у всех девочек были разного цвета волосы. Попробуй разгадать, у кого какой цвет волос, если сказано, что Маша не шатенка и не блондинка. А Карина не блондинка и не рыжая.»

Реши задачу: «Лежали конфеты в кучке: две матери, две дочки, да бабушка с внучкой взяли конфет по штучке и не стало этой кучки. Сколько было конфет в кучке?»

Б) Текстовые задачи.

Задания для ученического уровня:

Реши задачу: «В магазин привезли 240 кг фруктов. В пакетах было 90 кг фруктов, а в коробках – в 3 раза меньше, чем в пакетах, а остальные фрукты были в ящиках. Сколько фруктов было в ящиках?»

Реши задачу: «На столе учителя 120 тетрадей в клетку и 117 тетрадей в линейку. Учительница раздала 50 тетрадей. Сколько тетрадей у нее осталось?»

Задания для алгоритмического уровня:

Реши задачу. Запиши решение в виде числового выражения: «В магазин привезли 240 кг фруктов. В пакетах было 90 кг фруктов, а в коробках – в 3 раза меньше, чем в пакетах, а остальные фрукты были в ящиках. Сколько фруктов было в ящиках?»

Реши задачу. Подумай, можно ли решать задачу другим способом? «На столе учителя 120 тетрадей в клетку и 117 тетрадей в линейку. Учительница раздала 50 тетрадей. Сколько тетрадей у нее осталось?»

Задания для эвристического уровня:

Найди в задаче лишние данные. Измени условие и реши задачу: «В магазин привезли 240 кг фруктов в 3 пакетах, 2 ящиках и 6 коробках. В пакетах было 90 кг фруктов, а в коробках – в 3 раза меньше, чем в пакетах, а остальные фрукты были в ящиках. Сколько фруктов было в ящиках?»

Реши задачу двумя способами: «На столе учителя 120 тетрадей в клетку и 117 тетрадей в линейку. Учительница раздала 50 тетрадей. Сколько тетрадей у нее осталось?»

Задания для творческого уровня:

Измени вопрос и условие задачи так, чтобы общее количество конфет стало лишним данным. Запиши новую задачу и реши ее: «В магазин привезли 240 кг фруктов в 3 пакетах, 2 ящиках и 6 коробках. В пакетах было 90 кг фруктов, а в коробках – в 3 раза меньше, чем в пакетах, а остальные фрукты были в ящиках. Сколько фруктов было в ящиках?»

Измени задачу так, чтобы ее можно было решить тремя способами. Реши задачу тремя способами: «На столе учителя 120 тетрадей в клетку и 117 тетрадей в линейку. Учительница раздала 50 тетрадей. Сколько тетрадей у нее осталось?»

В) Задания геометрического характера

Задания для ученического уровня:

Найди периметр прямоугольника со сторонами 4 см и 8 см.

Начерти прямоугольник с длинами сторон 5 см и 3 см. Вычисли периметр этого прямоугольника.

Задания для алгоритмического уровня:

Начерти прямоугольник со сторонами 4 см и 8 см.

Найди периметр прямоугольника, если его ширина равна 8 см, а длина – на 22 см больше.

Задания для эвристического уровня:

Начерти прямоугольник со сторонами 4 см и 8 см. Найди его периметр.

От прямоугольника со сторонами 8 см и 12 см отрезали прямоугольник со сторонами 8 см и 9 см. Найди периметр оставшейся части. Начерти квадрат с таким же периметром.

Задания для творческого уровня:

Ширина прямоугольника 2 см, а его длина на 2 см больше. Начерти такой прямоугольник. Вычисли его периметр.

Длина ломаной из трёх звеньев 370 см. Найди длину третьего звена ломаной, если длина первого звена 15 дм, а длина второго звена равна 1/5 длины первого звена.

Г) Задания с величинами

Задания для ученического уровня:

Сравни:  2 ч 17 мин …2 ч;  3 ч … 180 мин; 7 сут … 1 неделя

Реши задачу: «На складе было 300 кг муки. Привезли еще 200 кг муки. Сколько килограмм муки стало на складе?»

Задания для алгоритмического уровня:

Сравни:  2 ч 17 мин … 1 ч 17 мин; 2 ч … 170 мин; 2 сут… 48 ч

Реши задачу: «На складе было 390 кг муки. Привезли еще 210 кг муки. Сколько килограмм муки стало на складе?»

Задания для эвристического уровня:

Найди значения выражений: 20 ч + 180 мин + 69 сек;  7 сут + 49 ч

Реши задачу: «На складе было 390 кг муки. Привезли еще 210 кг муки, а затем увезли 140 кг. Сколько килограммов муки осталось на складе?»

Задания для творческого уровня:

Найди значения выражений: 20 ч + 180 мин + 69 сек; 7 сут + 49 ч

Реши задачу: «На складе было 390 кг муки. Привезли еще 3 мешка по 70 кг муки в каждом, а затем со склада увезли 140 кг. Сколько килограмм муки осталось на складе?»

Д) Числа и вычисления

Задания для ученического уровня:

Составь все возможные трехзначные числа из предложенных цифр: 2, 0, 2.

Заполни пропуски: 400 – … = 400;  … – 500 = 0; 740 – 40 = …;  921 — … = 900

Задания для алгоритмического уровня:

Составь все возможные трехзначные числа из предложенных цифр: 0, 7, 3.

Заполни пропуски: 450 – … = 200; … – 300 = 150; 740 – 30 = …; 921 — … = 901

Задания для эвристического уровня:

Составь все возможные трехзначные числа из предложенных цифр: 3, 4, 5. Расположи полученные числа в порядке возрастания.

Заполни пропуски: 440 — … = 390; … — 130 = 270; 760 — … = 420; 580 — … = 410

Задания для творческого уровня:

Составь все возможные трехзначные числа из предложенных цифр и запиши их в порядке возрастания и убывания: 9, 7, 2.

Заполни пропуски: 448 — … = 395; … — 132 = 270; 766 — … = 422; 589 — … = 417

Е) Элементы алгебры

Задания для ученического уровня:

Реши уравнение:  20 + х = 320

Составь и реши уравнение: Неизвестное число уменьшили в 10 раз и получили 7

Задания для алгоритмического уровня:

Реши уравнение: 20 + х = 351

Составь и реши уравнение: Неизвестное число уменьшили на 190 и получили 720.

Задания для эвристического уровня:

Реши уравнение: 950 – х = 921

Составь и реши уравнения. Неизвестное число увеличили на 340 и получили 1000

Задания для творческого уровня:

Реши уравнение и полученный ответ запиши в виде суммы разрядных слагаемых:

900 – х = 184

Найди значение выражения а : 2 – а : 3, если а равно 762; 894

При решении разноуровневых дифференцированных заданий у детей могут возникнуть трудности. В таком случае со стороны учителя может быть оказана стимулирующая помощь (в начале и в конце работы), направляющая помощь (в процессе работы), обучающая помощь (от начала и до конца работы, отдельным ученикам). Помощь со стороны учителя не обязательно оказывается лично, так как могут быть использованы «карточки-помощницы». Например, при решении задачи 3-я и 4-я группы работают самостоятельно, а 1-ой и 2-ой группы предоставляются карточки с разной степени помощи. Карточки-помощницы могут содержать краткую запись, модель, схему, план решения, начало решения, частично выполненное решение, алгоритм решения задачи и так далее.

В ходе педагогического эксперимента мы выяснили, что использование дифференцированного подхода в обучении младших школьников математике будет эффективным при соблюдении следующих условий: задания должны быть подобраны с учетом индивидуальных особенностей учащихся; дифференцированные задания необходимо использовать на различных этапах урока; при выполнении учащимися дифференцированных заданий учителю следует организовать дифференцированную помощь; для достижения высоких результатов дифференцированный подход необходимо применять систематически.

 

Список литературы

 

1. Захарова, Т. Б. Профильная дифференциация обучения информатике на старшей ступени школы / Т. Б. Захарова. – М. : МЦНТИ, 2007. – 211 с.
2. Немов, Р. С. Психология образования: учеб. пособие для студентов / Р. С. Немов. — 2-е изд. – М. : Владос, 1998.

 

 

 

В статье содержательно представлена актуальность исследования, выводы подкреплены примерами. Представленные результаты эксперимента доказывают эффективность проделанной работы по проблеме исследования. Материал рекомендуется к публикации.