УДК 373.2.016:51:37.091.33-0.28.22
Шепелевич Варвара Александровна
студентка 3 курса психолого-педагогического факультета дневной формы обучения УО «Брестский государственный университет имени А. С. Пушкина», г. Брест
Научный руководитель – Л. В. Федорова, доцент кафедры общеобразовательных дисциплин и методик их преподавания БрГУ им. А. С. Пушкина
Когнитивно-визуальный подход в обучении математике как средство развития младших школьников
Современное начальное образование направлено на развитие всесторонне развитой личности ребенка. Это обуславливает поиск педагогамисовременных эффективных средств, методов и технологийобучения. Сегодня во многих психолого-педагогических исследованияхотмечено, что результативность обучения математике достигается посредством усиления принципа наглядности обучения. Так, В. А. Далингер отмечает: «Проблема реализации принципа наглядности в обучении математике может получить принципиально новое решение, если удастся найти такое методическое обеспечение деятельности ученика, которое позволит включать функции его визуального мышления для получения продуктивных результатов в овладении математическими понятиями, способами деятельности, для усиления развивающей функции наглядности» [3, с. 78]. При этом как подчеркивает, например Н. В. Бровка: «наглядность понимается шире, чем возможность зрительного восприятия» [2, с. 151]. Здесь за основу берется формирование визуального мышления, продуктом которого «является порождение новых образов, создание новых визуальных форм, несущих определенную смысловую нагрузку и делающих знание видимым» [4].
Как следствие, в обучении математике широкое применение находит когнитивно-визуальный подход, которыйосновывается на реализацию не иллюстративной функции наглядности, а именно познавательной. «Каждый учитель использует на уроке наглядный материал … Первая цельучителя состоит в том, чтобы ученик смотрел на предъявляемые ему зрительные образы. Этой цели достичь легко.Вторая цель состоит в том, чтобы ученик смотрел и виделто, что заложено в этих образах» [1].
Отмечается, что в начальной школе указанный подход наиболее действенный, так как обучение младших школьников математике строится именно на конкретных образах. Педагогами отмечается, что использование когнитивно-визуального подхода в педагогической практике способствует существенному развитиюмыслительных способностеймладших школьников.
Изучение математики в начальной школе посредством когнитивно-визуального подхода содействует формированию у учащихся способности осознанно оперировать математическими понятиями и суждениями, решать арифметические задачи. Например, именно познавательная визуализация позволяет младшим школьникам наглядно продемонстрировать отличительные особенности типовых арифметических задач, ключевые моменты их решения. При этом действенным средством такой визуализации выступают разнообразные модели (предметные, краткие записи, схемы, чертежи и прочие). Именно модели задачи позволяют ее визуализировать, органично соединяя ее текст и образ, усиливая при этом их когнитивное взаимодействие. Например, познавательная визуализация находит свое применение при выполнении упражнения на составление задач по предложенным моделям (рисунок 1). Для выполнения упражнения учащиеся должны «прочитать» чертежи (образы задач), проанализировать их, выявить отличительные особенности каждого (вид движения, данные и искомые величины), на основании чего представить тексты задач.
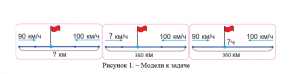
Также когнитивно-визуальный подход реализуется при выполнении учащимися упражнений на выбор правильной модели к задаче. Например, среди представленных на рисунке 2, схем выберите соответствующую следующей задаче: «Масса пяти пачек творога на 510 г меньше массы восьми таких пачек. Найди массу пяти пачек с творогом» [6, с. 45].
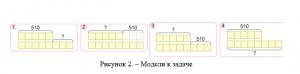
Применение разнообразных моделей позволяет сформировать для учащихся полную картину всех типовых задач, выявить способы их решения, что способствует прочному и осознанному обучению младших школьников решению не только типовых, но и любых арифметических задач.
Таким образом, обучение математике в начальной школе, которое основывается на когнитивно-визуальном подходе, заключается в активизации именно познавательной функции наглядности, что способствует целенаправленному переносу акцента с обучающей на развивающую функцию обучения. В свою очередь важно отметить, что реализация когнитивно-визуального подхода в начальном обучении математике возможна только при постоянном, систематическом и целенаправленном использовании разнообразных средств наглядности на каждом этапе процесса обучения, которые учащиеся будут не столько наблюдать, сколько «читать».
Библиографический список
- Башмаков,М. И. Развитие визуального мышления на уроках математики / М. И. Башмаков, Н. А. Резник // Математика в школе. – 1991. – № – С. 4–8.
- Бровка,Н. В. Интеграция теории и практики обучения математике как средство повышения качества подготовки студентов / Н. В. Бровка. – Минск : БГУ, 2009. – 243 с.
- Евразийская педагогическая конференция: сборник статей II Международной научно-практической конференции. – Пенза : МЦНС «Наука и Просвещение». – 2018. – 166 с.
- Зинченко,В. П. Формирование зрительного образа. Исследование деятельности зрительной системы / В. П. Зинченко, Н. Ю. Вергелес. – М. : Изд-во МГУ, 1969. – 106 с.
- Мордкович,А. Г. Методические проблемы изучения элементов математического анализа в общеобразовательной школе // Математика в школе, 2002. – № – С. 2–12.
- Муравьева,Г. Л.Математика : учебное пособие для 4 класса учреждений общего среднего образования с русским языком обучения/Г. Л. Муравьева, М. А. Урбан : в 2 частях. – Ч. 2. – Минск : Национальный институт образования, 2022. – 136 с.

