Вахильчук О.В. ИСПОЛЬЗОВАНИЕ ПАЛОЧЕК КЮИЗЕНЕРА В ПРЕДМАТЕМАТИЧЕСКОЙ ПОДГОТОВКЕ ДОШКОЛЬНИКОВ

Одним из направлений подготовки дошкольников к школе является формирование у них элементарных математических представлений в процессе освоения предматематики.

Этот процесс связан со всеми сторонами воспитательно-образовательной работы дошкольного учреждения (ДОУ) и направлен, прежде всего, на решение задач умственного воспитания и математического развития дошкольников. Отличительными его чертами являются общая развивающая направленность, связь с умственным, речевым развитием, игровой, бытовой, трудовой деятельностью [1].

Организация предматематической подготовки изложены в трудах отечественных (П. Я. Гальперин, В. С. Давыдов, З. А. Михайлова, А. А. Столяр, А. Д. Соловьева, А. В. Белошистая, Т. С. Будько, А. Н. Носова, И. В. Житко, Л. Г. Петерсон, А. К. Артемов и др.) и зарубежных педагогов (Ж. и Ф. Папи, М. Фидлер, Д. Альтхауз, Э. Дум, Р. Грин, В. Лаксон и др.).

Существует 5 основных задач предматематической подготовки детей в ДОУ [1]: формирование системы элементарных математических представлений у дошкольников; формирование предпосылок математического мышления и отдельных логических структур; формирование сенсорных процессов и способностей (в дошкольном возрасте осуществляется освоение сенсорных эталонов не только не перцептивном, но и на интеллектуальном уровне (Л. А. Венгер) [2] ); расширение словаря детей и совершенствование связной речи; количественные отношения, которые осознаются в результате действий при сравнении отдельных предметов и их совокупностей. Эти задачи решаются не изолированно, а комплексно, в процессе специально организованной игровой деятельности.

Игра, являясь ведущим видом деятельности дошкольников, позволяет организовать предматематическую подготовку благодаря использованию специальных дидактических пособий. Одним из таких пособий являются набор палочек Кюизенера. Набор содержит  палочки десяти цветов, включая 241 палочку. Палочки различных цветов имеют разную длину — от 1 до 10 см. Каждая палочка — это число, выраженное цветом и величиной, то есть длиной в сантиметрах. Близкие друг другу по цвету, палочки объединяются в одно «семейство», или класс [3]. Палочки дают возможность выполнять упражнения и в горизонтальной, и в вертикальной плоскости.

Возможности палочек Кюизенера достаточно широки. Игры с использованием набора развивают творческие способности, воображение, фантазию, способность к моделированию и конструированию, воспитывают самостоятельность, инициативу и настойчивость в достижении цели. Благодаря играм у ребенка развиваются все психические процессы, мыслительные операции, формируются представления о математических понятиях. С помощью палочек Кюизенера можно еще в детском саду познакомить детей с арифметической прогрессией, своеобразной «цветной алгеброй», готовящей к изучению школьной алгебры [4].

Несмотря на то, что палочки Кюизенера просты в изготовлении и знакомы педагогам,  в практике дошкольной подготовки они практически не используются. С целью выявления возможностей данного пособия в совершенствовании  предматематической подготовки в условиях работы по действующей программе, мы провели исследование на базе ГУО «Ясли-сад агрогородка Обухово» в 2013 году.

В исследовании принимали участие две однородные группы, каждая из которых насчитывала по десять детей в возрасте 4-5 лет: экспериментальная (средняя группа № 6) и контрольная  (средняя группа № 9).

На констатирующем этапе эксперимента уточнялся уровень сформированности математических представлений детей. Для этого были разработаны диагностические игры и упражнения: игры подготовительного этапа, целью которых являлось знакомство с набором палочек;  игры, способствующие усвоению эталонов цвета; игры на  изучение отношений  «высокий — низкий»,  «широкий -  узкий»,  «длинный – короткий», «тонкий – толстый»; игры и упражнения на развитие у детей количественных представлений.

Рассмотрим некоторые упражнения: найди и покажи палочку такую же по цвету и по длине; отбери все красные (синие, желтые и т. д.), палочки такой же длины; перечисли все цвета всех палочек на столе; сопоставь палочки одновременно по цвету и длине; сравни  палочки по цвету; найти и покажи самую короткую и длинную палочку и назови ее цвет; выбери две палочки и найти среди них длинную (короткую); построй  дом, отбирая для стен — красные палочки, желтые — для крыши, розовую — для трубы; построй поезд, начиная с самого длинного вагона (или наоборот, с  короткого); сделай из 4 желтых палочек стул, рядом расположи большой стол; возьми в правую руку столько палочек, сколько можешь удержать.

Результаты выполнения заданий анализировались по следующим показателям: активность ребёнка в деятельности с цветными счётными палочками Кюизенера; творческие проявления; принятие ребёнком ведущей роли в играх и упражнениях.

Анализ результатов констатирующего эксперимента (таблицы 1 и 2) показал, что уровень освоения математических представлений детьми экспериментальной группы ниже, чем у детей контрольной группы, а также ниже возможного для детей среднего дошкольного возраста (преимущественно средний уровень). Это проявилось в активности детей в деятельности с палочками Кюизенера. У многих детей понижена самостоятельность, требовалось подключение взрослого к процессу: повторное объяснение упражнения, советы, указания, наводящие вопросы. Наблюдалась сниженная творческая инициатива, дети опирались на уже имеющийся опыт оперирования палочками при выполнении задания, не проявляя желания предложить другой вариант.

Таблица 1 – Результаты диагностики в экспериментальной группе на констатирующем этапе эксперимента

ФИО	Диагностические упражнения				Уровень сформированности математических представлений у дошкольников
	Подготовительные	Усвоение эталонов цвета	Отношения «высокий — низкий» , «длинный-короткий» и др.	Количественные представления
Петя Б.	8	9	9	8	Высокий
Рита С.	8	9	9	8	Высокий
Надя Д.	6	5	4	5	Средний
Кира С.	6	5	4	5	Средний
Элла К.	3	3	3	3	Низкий
Саша Р.	7	7	5	6	Средний
Саша З.	7	7	7	7	Средний
Ваня П.	3	3	3	2	Низкий
Юра К.	3	3	2	3	Низкий
Оля В.	7	7	7	7	Средний

Таблица 2 – Результаты диагностики в контрольной группе на констатирующем этапе эксперимента

ФИО	Диагностические упражнения				Уровень сформированности математических представлений у дошкольников
	Подготовительные	Усвоение эталонов цвета	Отношения «высокий — низкий» , «длинный-короткий» и др.	Количественные представления
Юля Б.	8	9	9	8	Высокий
Оля С.	8	9	9	8	Высокий
Катя Д.	6	5	4	5	Средний
Глеб С.	6	5	4	5	Средний
Рита К.	3	3	3	3	Низкий
Ваня Р.	8	8	9	9	Высокий
Рома З.	3	3	3	3	Низкий
Юра П.	8	8	8	8	Высокий
Боря К.	7	7	6	5	Средний
Лена В.	9	8	8	8	Высокий

На формирующем этапе эксперимента мы проводили целенаправленную предматематическую подготовку с использованием палочек Кюизенера. Сначала набор применяли для игр конструктивного характера. Дети с удовольствием строили различные фигуры, выкладывали узоры и картинки, сопровождаемые  сюжетом. Свобода действий способствовала проявлению фантазии.  В ходе манипулирования палочками мальчики, в основном, строили дороги и гаражи, машины и поезда, башни и лесенки. Девочки увлекались составлением мозаик и узоров, сюжетных картинок (рисунок 1).

Рассмотрим примеры некоторых упражнений: положи столько же  палочек  и такого же цвета, сколько у меня; определи, что изменилось в ряду палочек (после того, как их поменяли местами или убрали из ряда одну  палочку); с помощью красной  палочки  измерь длину окружающих предметов:  кровати,  стола,  книги; с закрытыми глазами найди две  палочки  разной длины; покажи некрасную палочку.

Затем проводились игры, в ходе которых дети учились «чувствовать» числа. Рассмотрим примеры некоторых из них.

- Предлагается найти самую короткую  палочку. Уточняется, какого она цвета. Белая  палочка  — это единица, число «один». К каждой цветной  палочке  подбирается ее аналог, изображенный на карточке – числовой фигуре.

- Предлагается построить необычный поезд из цветных палочек, посадить в вагончики пассажиров и узнать,  сколько мест  в каждом в вагончике. Дети находят ответ практическим путем: берут белые палочки и накладывают на вагончики каждого цвета (рисунок 1).

Рисунок 1 – Работа с палочками Кюизенера

В ходе игровых упражнений мы называли число — ребенок находил палочку соответствующего цвета. Вначале числа называли по порядку, далее – вразбивку. Для закрепления знаний цветовой гаммы после игры детям предлагалось сложить все палочки в одну общую большую коробку в определенной цветовой последовательности: сначала все белые палочки, потом розовые и т.д.

Игровые упражнения с палочками Кюизенера проводились как индивидуально, так и с небольшими группами по несколько детей. Для поднятия интереса к игровой деятельности с палочками Кюизенера использовались элементы соревнования.

По мере того, как дети хорошо освоили палочки Кюизенера, работа с ними перешла в форму выполнения упражнений, проигрывание игровых ситуаций. Для закрепления устойчивого интереса, были придуманы награды-символы: «Лучшему конструктору», «Самому старательному!», — которые вручались детям-победителям по итогам подводимым в конце игры. Многие игры и упражнения со счетными палочками несли проблемно-практический характер: хватит ли палочек-бревнышек для домика мышки? Это вызывало у детей интерес, сочувствие и искреннее желание помочь героям, давало толчок к активной самостоятельной поисково-творческой деятельности.

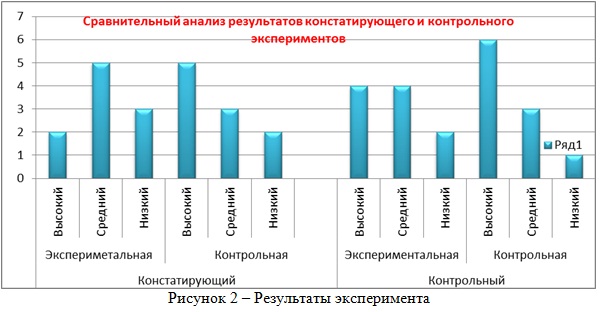
На третьем этапе эксперимента – контрольном – была проведена итоговая диагностика. Результаты диагностики таковы: в экспериментальной группе 4 ребенка продемонстрировали высокий уровень; средний уровень показали 4 ребенка;  низкий уровень – 2 ребенка. В контрольной группе высокий уровень у 6 детей; средний уровень показали 3 ребенка; низкий уровень – 1 ребенок. Сравнительный анализ результатов констатирующего и контрольного экспериментов представлен в диаграмме (рисунок 2).

Исходя из итоговой диагностики можно сделать следующие выводы:

1) Анализ результатов исследования показал, что уровень освоения детьми экспериментальной группы математических представлений в деятельности с палочками Кюизенера  стал выше по сравнению с результатами входной диагностики.  В контрольной группе также произошел прирост, однако результаты в экспериментальной группе более значимы, потому что группа является интегрированной.

2) Полученные результаты подтвердили значимость проведенной работы и эффективность применения палочек Кюизенера для развития математических представлений у дошкольников.

Таким образом, целенаправленная работа по использованию палочек Кюизенера способствует формированию количественных, пространственных и величинных представлений.

Список литературы