Карпейчик М.И. ТОЧКИ, ЛИНИИ, ТРЕУГОЛЬНИК

Приступая к работе, мы поставили цель: вспомнить теоремы геометрии, которые были предметом нашего изучения, постараться взглянуть на них в целом, увидеть в них что-то общее, объединяющее и оформить в виде небольшого, цельного фрагмента. В качестве объекта исследования мы выбрали одну из простейших геометрических фигур – треугольник. Его элементы обладают целым рядом замечательных свойств. Многие из них были известны за несколько столетий до нашей эры, другие открыты в 19 веке. Исследования продолжаются. Ведь каждое свойство – это закономерность ,которая может быть использована другими науками в практических целях. Например: физическое понятие «центр тяжести треугольной пластинки» связано с понятием «точка пересечения медиан треугольника». Другие же свойства могут представлять чисто теоретический интерес, но на их основе устанавливаются «практические» свойства. Поиск в науке продолжается.

Другая цель, вытекающая из первой, заключалась в том, чтобы подчеркнуть внутреннюю стройность геометрических утверждений, гармонию и красоту геометрических построений. Ведь «геометрия сохранила всегда присущую ей эстетическую привлекательность, и не поблекла красота ее результатов» [1, с. 12].

И третья цель – дополнить известные свойства, связанные с треугольником, еще одним свойством (еще одной точкой и прямой), по сути, не известным ни ученикам, ни учителям.

Рассмотрим произвольный треугольник и самые известные связанные с ним точки и линии: высоты, биссектрисы, медианы, центр окружности, описанной около треугольника, центр окружности, вписанной в треугольник, ортоцентр. Расскажем об окружности девяти точек и дополним ее десятой точкой.

Ортотреугольник

Треугольник, вершинами которого являются основания высот данного, называется  ортотреугольник.

Треугольник АВС – произвольный остроугольный треугольник. АD, ВЕ, CF – его высоты. Точка H – точка пересечения высот треугольника – ортоцентр. Треугольник DEF,вершинами которого являются основания высот, называется ортотреугольником. Точка О – центр окружности, описанной около треугольника ABC.

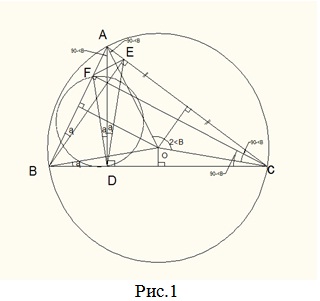
О многом можно узнать, если рассмотреть этот рисунок:

Окр. (DHEC):

= DH -биссектриса

Аналогично:

EH- биссектриса

FH – биссектриса

Первый интересный вывод: Высоты треугольника являются биссектрисами углов его ортотреугольника.

Второй вывод: Биссектрисы внутренних углов треугольника пересекаются в одной точке.

Третий вывод: Ортоцентр треугольника является центром окружности, вписанной в ортотреугольник.

Четвертый вывод: Прямая, проходящая через основания высот треугольника, отсекает треугольник, подобный данному.

Пятый вывод: Высота треугольника и радиус описанной окружности, проведенные из одной вершины, образуют равные углы со сторонами треугольника.

Шестой вывод: Биссектриса угла треугольника делит пополам угол между высотой и радиусом описанной окружности, проведенными из одной вершины и др.

Серединный треугольник

Серединный треугольник – это треугольник, вершинами которого является середины сторон данного треугольника.

Рассмотрим произвольный остроугольный треугольник АВС:

AD,BE ,CM –высоты треугольника

,  ,  –медианы треугольника

 Точка H – ортоцентр треугольника

Точка O – центр окружности, описанный около треугольника АВС.

Треугольник – серединный треугольник, его вершинами являются середины сторон треугольника АВС.

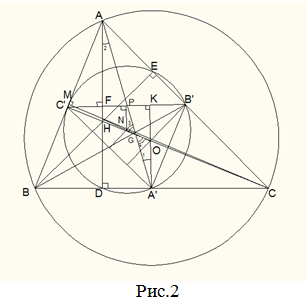
Сделаем некоторые выводы, рассматривая этот рисунок.

1. Так как стороны ,то треугольники ,сторонами которых являются стороны треугольников АВС и подобны
2. , значит, коэффициент подобия равен и отношение соответствующих линейных элементов равно .
3. Точка P делит отрезок пополам. Поэтому медианы треугольника  совпадают с медианами треугольника АВС. Следовательно, точка пересечения медиан треугольников единая.
4. Высоты серединного треугольника являются серединными перпендикулярами к сторонам основного. Отсюда следует вывод, что ортоцентр серединного треугольника совпадает с центром окружности, описанной около основного.
5. Точка Н – ортоцентр треугольника АВС, точка О – ортоцентр треугольника , подобного АВС. Тогда, с учетом вывода п.2, АН=
6. И, наконец, сделаем еще один важный вывод: точки H, N,G лежат на одной прямой, которая называется прямой Эйлера.

Для этого достаточно показать, что  ,значит, они будут вертикальными при прямой и точки H, N,G принадлежат прямой, причем точка G делит отрезок НО на две части так, что .

Окружность девяти точек

Продолжая рассматривать рисунок 2,можно легко заметить, что основания высот и середины сторон треугольника лежат на одной окружности с центром в точке N, которая делит отрезок между точкой пересечения высот и центром описанной окружности пополам. Более того, оказывается, что эта окружность делит отрезки, соединяющие вершины треугольника с точкой пересечения его высот пополам. Эта окружность получила  название окружности девяти точек. Её еще называют окружность Эйлера. Рис.3

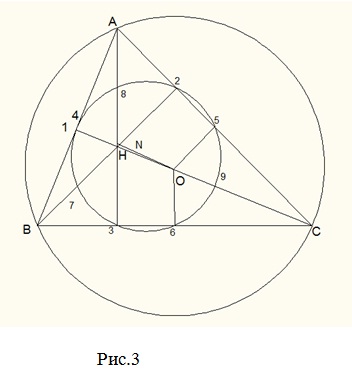
Если внимательно рассмотреть рисунки 1,2 и рисунок 3,то можно заметить удивительные свойства, которые связывает ортотреугольник и серединный треугольник имеют общую описанную окружность. Этот факт был доказан Л. Эйлером в 1765 году.

Точка Цвойдзинского

Дополним наш обзор некоторых свойств элементов треугольника, связанных между собой.

Рассмотрим произвольный остроугольный треугольник АВС и произвольную прямую. Оказывается:

Если из вершин треугольника АВС опустить перпендикуляры  на произвольную прямую а, лежащую в плоскости треугольника, из оснований этих перпендикуляров  вновь опустить перпендикуляры на стороны  ВС,АС,АВ, то они пересекутся в одной точке М.

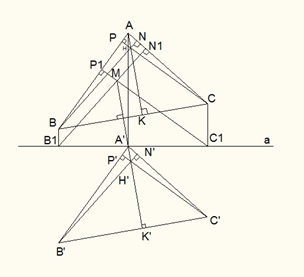
В статье П.Фалеева(2,с.173-181) точка М названа точкой Цвойдзинского. Однако в письме учителя математики Дм.Ефремова, опубликованном в «Вестнике опытной физики и элементарной математики» (№ 331, XXVIII, семестр № 7, с. 158), говорится что «теоремы, связанные с этой точкой, были доказаны ранее известными математиками: Neuberg-ом,Aubel-ем,Soons-ом. Поэтому это не точка Цвойдзинского, а Souns-а,..»

Нас интересует, существует ли связь между точкой Цвойдзинского и теми замечательными точками и линиями, которые рассмотрены в предыдущих фрагментах. Ведь прямая а – произвольная прямая. Значит, она может занимать и какое-то частное положение относительно элементов треугольника. А следовательно, и точка М будет перемещаться в плоскости треугольника.

Такая связь существует. Она  характеризуется следующим утверждением: если прямая а будет проходить через центр окружности, описанной около треугольника АВС, то при всех положениях прямой а, соответствующая ей точка М будет находиться на окружности девяти точек.

Итак, рассмотренные нами свойства замечательных точек и прямых треугольника, показывают, насколько глубока внутренняя связь между различными элементами геометрических фигур, их гармония и красота. Геометрия изучает объекты окружающего нас мира, законы природы на своем языке: «Природа говорит языком математики; буквы этого языка – круги, треугольники и иные математические фигуры», — говорил Галилео Галилей. И на этом языке мы говорим о красоте нашей природы.

Таким образом, десять точек, полученных в результате различных, казалось бы, не связанных между собой построений, располагаются на одной окружности. Известный советский методист В.Г. Болтянский утверждает: «красота – это наглядность плюс неожиданность». Да, с неожиданность плюс внутренняя гармония заставляет десять точек располагается на одной окружности.

Список используемых источников