УДК: 74.202.66

Цагельник Е.И.

 

магистрант педагогического факультета

УО «Гродненский государственный университет имени Янки Купалы», г. Гродно

 

(научный руководитель – Т. М. Гимпель, старший преподаватель кафедры естественнонаучных и лингвистических дисциплин и методик их преподавания)

 

АРИФМЕТИЧЕСКИЕ ТЕКСТОВЫЕ ЗАДАЧИ В МАТЕМАТИЧЕСКОЙ ПОДГОТОВКЕ МЛАДШИХ ШКОЛЬНИКОВ

 

Аннотация. В статье раскрываются основные вопросы методики работы над арифметическими текстовыми задачами на I ступени общего среднего образования.

 

Решение текстовых задач на уроках математики на I ступени общего среднего образования играет важную роль в обучении учащихся. При решении задачи младшие школьники приобретают новые знания, их углубляют, систематизируют, закрепляют. Умение решать задачи является показателем уровня математического развития, глубины усвоения учебного материала.

Существуют различные подходы к определению текстовой арифметической задачи [1]. Отметим некоторые из них:

1. В окружающей нас жизни возникает множество таких ситуаций, которые связаны с числами и требуют выполнения арифметических действий над ними, – это задачи (М. А. Бантова) [2, с. 116].
2. Задача – это сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий (М. И. Моро, А. М. Пышкало) [3, с. 96].
3. Текстовая задача есть описание некоторой ситуации (ситуаций) на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между его компонентами или определить вид этого отношения (Л. П. Стойлова, А. М. Пышкало) [4, с. 234].
4. В начальном курсе математики понятие «задача» обычно используется тогда, когда речь идет об арифметических задачах. Они формулируются в виде текста, в котором находят отражение количественные отношения между реальными объектами (Н. Б. Истомина) [5, с. 198].
5. Под текстовыми арифметическими задачами подразумевают задачи, имеющие житейское, физическое содержание и решаемые с помощью арифметических действий (В. Л. Дрозд) [6, с. 156].

Таким образом, можно утверждать, что четкого определения понятия «арифметическая задача» не существует.

Решить задачу в широком смысле – значит раскрыть связи между данными и искомым, заданные условием задачи, на основе чего выбрать, а затем выполнить арифметические действия и дать ответ на вопрос задачи [2, с. 179].

В школьном курсе математики чаще всего используют арифметический и алгебраический способы решения задач. При арифметическом способе ответ на вопрос задачи находится путем выполнения арифметических действий, алгебраический предполагает составление и решение уравнения. Кроме того, на уроках математики на I ступени общего среднего образования применяются графический и практический способы решения задач. Они не требуют выполнения арифметических действий. При графическом способе используются чертежи, для практического достаточно уметь считать.

Рассмотрим эти способы решения на примере конкретной задачи: «Девять конфет разложили по 3 на несколько тарелок. Сколько тарелок понадобится?».

• Арифметический способ: 9 : 3 = 3.
• Алгебраический способ. Младшие школьники рассуждают следующим образом: количество тарелок у нас неизвестно, значит, обозначим его x. Из условия задачи мы знаем, что на каждой тарелке по 3 конфеты, значит все количество конфет – 3×x. Так как всего конфет 9, то можно составить уравнение 3×x= 9.
• Графический способ. Изобразим каждую конфету отрезком, а каждую тарелку покажем дугой. Получим:

  

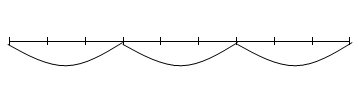
• Для решения задачи практическим способом необходимо иметь 9 конфет. Последовательно положим по 3 конфеты на каждую тарелку. Затем ответим на вопрос задачи, посчитав количество заполненных тарелок.

Каждый из выше представленных способов решения задачи имеет свои как положительные, так и отрицательные стороны. К примеру, графический способ требует развитого абстрактного мышления и не воспринимается учащимися с низкой успеваемостью.

Решение текстовых арифметических задач на I ступени общего среднего образования не сводится только к получению ответа. В процессе работы над задачей раскрывается конкретный смысл арифметических действий, выполняются табличные или внетабличные вычисления, вводятся рациональные приемы вычислений и соответствующие им правила.

Выделяют следующие этапы работы над задачей, которые должны строго соблюдаться [7]:

1. Усвоение содержания задачи. На данном этапе от учащихся требуется понять задачу, выделить условие и установить связи между данными.
2. Разбор задачи или поиск решения. Цель – составление плана решения.
3. Решение задачи. Младшие школьники оформляют решение и записывают ответ.
4. Проверка решения.

При обучении младших школьников решению арифметических текстовых задач необходимо использовать творческие виды работы над задачей [7]:

1. Составление условия к вопросу.

Учитель предлагает учащимся составить условие к конкретному вопросу. К примеру, «Сколько цветов в двух вазах?». Младшие школьники рассуждают следующим образом: «Для того чтобы узнать, сколько цветов в двух вазах, необходимо знать, сколько цветов в каждой вазе в отдельности». При этом целесообразно использовать наглядный материал. В качестве наглядности можно использовать различный раздаточный материал (карандаши, ручки, счетные палочки). Присоединив карандаши из одной стопки в другую, исключая возможность их пересчитывания, учащиеся записывают решение математическими знаками, тем самым отвечают на поставленный вопрос.

2. Составление вопроса к условию.

На основе имеющихся в задаче данных младшим школьникам предлагается составить подходящий вопрос. К примеру, «На одной тарелке 6 яблок, а на другой – на 3 яблока меньше». Учащиеся должны определить, что значит на 3 яблока меньше? На какой тарелке яблок больше, а на какой меньше? Как узнать число яблок на второй тарелке? Какой вопрос можно поставить к условию, чтобы получить задачу? Такой вид работы направлен на формирование умения анализировать данные условия задачи.

3. Решение задач с лишними данными.

К примеру, «На ветке сидело 8 ласточек. Улетели 3 ласточки, а потом еще 2 прилетели. Сколько ласточек улетело?». В ходе решения таких задач младшие школьники сталкиваются с реальной ситуацией, которая требует внимательного отношения к анализу текста задачи.

4. Решение задач с недостающими данными.

К примеру, «У Тони 4 карандаша. Сколько всего карандашей у Тони и Кати?». В процессе этой работы от учащихся требуется проведение определенного анализа условия задачи. Им необходимо определить, что необходимо знать, чтобы ответить на вопрос задачи.

5. Составление задачи, обратной данной.

Такой вид работы над задачей целесообразно использовать для проверки правильности решения. К примеру, «Летние каникулы длились 92 дня. Из них 30 дней Петя провел в городе, а остальные – в деревне. Сколько дней Петя провел в деревне?». После анализа данной задачи и её решения учащиеся составляют задачу, обратную данной: «Летние каникулы продолжались 92 дня. Несколько дней Петя провел в городе, а 62 дня – в деревне. Сколько дней Петя провел в городе?» или «30 дней летних каникул Петя провел в городе, а 62 дня – в деревне. Сколько дней продолжались летние каникулы?».

6. Решение логических задач, задач на смекалку.

К примеру, «Каждая из девочек – Маша и Света – пошла в кино со своей мамой. Сколько человек пошли в кино?». Вариантов ответа может быть два: трое или четверо. При условии, что девочки родные сестры и мама у них одна, в кино пойдут 3 человека. А если девочки подруги, то в кино пойдут 4 человека.

Решение таких задач направлено на развитие логического мышления, наблюдательности. В них ярко выражена связь с жизненной ситуацией.

С целью выявления значимости творческих видов работы над задачей в первом классе нами в 2016-2017 учебном году было проведено исследование на базе 1 «Е» класса ГУО «Средняя школа № 40 г. Гродно». Ученикам была предложена разноуровневая самостоятельная работа. По ее результатам 15 % учащихся допустили ошибки в решении текстовой задачи.

Количественный и качественный анализ допущенных ошибок показал, что младшие школьники неправильно интерпретировали условие задачи, многие не смогли правильно установить связи между данными. Учитывая это, при работе над ошибками мы применяли следующие виды работы: составление другой задачи по вопросу данной; составление аналогичной задачи, но с другими числовыми данными и другим сюжетом; составление и решение задачи по чертежу и другие. В ходе повторного проведения самостоятельной работы оказалось, что с решением текстовой задачи не справились лишь 7 % учащихся.

Таким образом, при обучении решению арифметических текстовых задач необходимо использовать как можно больше разнообразных видов творческой работы над задачей. Это способствует развитию у младших школьников памяти, мышления, творческого воображения, внимания, наблюдательности; учит рассуждать последовательно, четко, кратко и правильно излагать свои мысли, обосновывать выводы.

 

Список литературы

1. Овчинникова, М. В. Методика работы над текстовыми задачами в начальных классах (общие вопросы) : учеб.-метод. пособие для студ. спец-тей «Начальное обучение. Дошкольное воспитание» / М. В. Овчинникова. – К. : Пед. пресса, 2001. – 128 с.
2. Бантова, М. А. Методика преподавания математики в начальных классах / М. А. Бантова, Г. В. Бельтюкова. – М. : Просвещение, 1984. – 335 с.
3. Моро, М. И. Методика обучения математике в 1–3 классах / М. И. Моро, А. М. Пышкало. – М. : Просвещение, 1975. – 336 с.
4. Стойлова, Л. П. Основы начального курса математики / Л. П. Стойлова, А. М. Пышкало. – М. : Просвещение, 1988. – 320 с.
5. Истомина, Н. Б. Методика обучения математике в начальных классах : учеб. пособие для студ. сред. и высш. учеб. заведений. – М. : Академия, 1998. – 288 с.
6. Методика начального обучения математике / Под общ. ред. А. А. Столяра, В. Л. Дрозда. – Минск : Выш. школа, 1988. – 254 с.
7. Роль текстовых задач в начальном обучении математике [Электронный ресурс]. – Режим доступа: http://festival.1september.ru/articles/573133/. – Дата доступа: 12.04.2017.